Policy evaluation with adaptively generated data. — output

Calculates average response and differences in average response under counterfactual treatment policies. Estimates are produced using provided inverse probability weighted (IPW) or augmented inverse probability weighted (AIPW) scores paired with various adaptive weighting schemes, as proposed in hadad2021confidence;textualbanditsCI and zhan2021off;textualbanditsCI.

We briefly outline the target quantities: For observations indexed $t \in \{1,\dots,A\}$, treatments $w \in \{1,\dots,K\}$, we denote as $Y_t(w)$ the potential outcome for the unit at time $t$ under treatment $w$. A policy $\pi$ is a treatment assignment procedure that is the subject of evaluation, described in terms of treatment assignment probabilities for each subject to receive each counterfactual treatment. We target estimation of average response under a specified policy: $$Q(\pi) := \sum_{w = 1}^{K}\textrm{E}\left[\pi(w)Y_t(w)\right]$$ The user may specify a list of list of policies to be evaluated, under policy1.

Alternatively, they may estimate policy contrasts if policy0 is provided: $$\Delta(\pi^1,\pi^2) := Q(\pi^1) - Q(\pi^2) $$

Usage

output_estimates(
  policy0 = NULL,
  policy1,
  contrasts = "combined",
  gammahat,
  probs_array,
  uniform = TRUE,
  non_contextual_minvar = TRUE,
  contextual_minvar = TRUE,
  non_contextual_stablevar = TRUE,
  contextual_stablevar = TRUE,
  non_contextual_twopoint = TRUE,
  floor_decay = 0
)

Arguments

policy0: Optional matrix. Single policy probability matrix for contrast evaluation, dimensions [A, K]. Each row represents treatment assignment probabilities for an individual subject, and so rows must sum to 1. When policy0 = NULL, the function estimates the value $Q(\pi)$ of each policy matrix listed in policy1. When policy0 is non-null, the function estimates differences in average response under each of the component policies in policy1 and the single policy in policy0. Must not contain NA values if provided.
policy1: List of matrices. List of counterfactual policy matrices for evaluation, dimensions [A, K]. Each row represents treatment assignment probabilities for an individual subject, and so rows must sum to 1. Must not contain NA values.
contrasts: Character. The method to estimate policy contrasts, either combined or separate, discussed in hadad2021confidence;textualbanditsCI Section 3. combined indicates the difference in (A)IPW scores is directly used as the unbiased scoring rule for $\Delta (\pi^1, \pi^2)$; separate indicates that scores are used separately $\hat \Delta (\pi^1, \pi^2) = \hat Q (w_1) - \hat Q (w_2)$.
gammahat: (A)IPW scores matrix with dimensions [A, K] in non-contextual settings, or [A, A, K] contextual settings. Dimensions represent time, (contexts,) treatment arms. Dimensions of gammahat and probs_array must be the same. Must not contain NA values.
probs_array: Numeric array. Probability matrix or array with dimensions [A, K] in non-contextual settings, or [A, A, K] contextual settings. Dimensions represent time, (contexts,) treatment arms. Dimensions of gammahat and probs_array must be the same. Must not contain NA values.
uniform: Logical. Estimate uniform weights.
non_contextual_minvar: Logical. Estimate non-contextual MinVar weights described in zhan2021off;textualbanditsCI Section 4.
contextual_minvar: Logical. Estimate contextual MinVar weights described in zhan2021off;textualbanditsCI Section 4.
non_contextual_stablevar: Logical. Estimate non-contextual StableVar weights described in zhan2021off;textualbanditsCI Section 4.
contextual_stablevar: Logical. Estimate contextual StableVar weights described in zhan2021off;textualbanditsCI Section 4.
non_contextual_twopoint: Logical. Estimate two-point allocation weights described in hadad2021confidence;textualbanditsCI Section 2.
floor_decay: Numeric. Floor decay parameter used in the calculation. Default is 0.

Value

A list of treatment effect estimates under different weighting schemes.

References

hadad2021confidencebanditsCI

zhan2021offbanditsCI

Examples

set.seed(123)
# In a non-contextual setting, generate example values for policy1, gammahat, and probs_array
gammahat <- matrix(c(0.5, 0.8, 0.6,
                     0.3, 0.9, 0.2,
                     0.5, 0.7, 0.4,
                     0.8, 0.2, 0.6), ncol = 3, byrow = TRUE)
policy0 <- matrix(c(1, 0, 0,
                    1, 0, 0,
                    1, 0, 0,
                    1, 0, 0), ncol = 3, byrow = TRUE)
policy1 <- list(matrix(c(0, 1, 0,
                         0, 1, 0,
                         0, 1, 0,
                         0, 1, 0), ncol = 3, byrow = TRUE))

probs_array <- array(0, dim = c(4, 4, 3))
for (i in 1:4) {
  temp_vector <- runif(3)
  normalized_vector <- temp_vector / sum(temp_vector)
  probs_array[i, 1, ] <- normalized_vector
}
for (k in 1:3) {
  for (i in 1:4) {
    temp_vector <- runif(3)
    normalized_vector <- temp_vector / sum(temp_vector)
    probs_array[i, 2:4, k] <- normalized_vector
  }
}
estimates <- output_estimates(policy1 = policy1,
                              policy0 = policy0,
                              gammahat = gammahat,
                              probs_array = probs_array)
# plot
plot_results <- function(result) {
  estimates <- result[, "estimate"]
  std.errors <- result[, "std.error"]
  labels <- rownames(result)

  # Define the limits for the x-axis based on estimates and std.errors
  xlims <- c(min(estimates - 2*std.errors), max(estimates + 2*std.errors))

  # Create the basic error bar plot using base R
  invisible(
    plot(estimates, 1:length(estimates), xlim = xlims, xaxt = "n",
         xlab = "Coefficient Estimate", ylab = "",
         yaxt = "n", pch = 16, las = 1, main = "Coefficients and CIs")
  )

  # Add y-axis labels
  invisible(
    axis(2, at = 1:length(estimates), labels = labels, las = 1, tick = FALSE,
         line = 0.5)
  )

  # Add the x-axis values
  x_ticks <- x_ticks <- seq(from = round(xlims[1], .5),
                            to = round(xlims[2], .5), by = 0.5)
  invisible(
    axis(1,
         at = x_ticks,
         labels = x_ticks)
  )

  # Add error bars
  invisible(
    segments(estimates - std.errors,
             1:length(estimates),
             estimates + std.errors,
             1:length(estimates))
  )
}

sample_result <- estimates[[1]]
op <- par(no.readonly = TRUE)
par(mar=c(5, 12, 4, 2))
plot_results(sample_result)

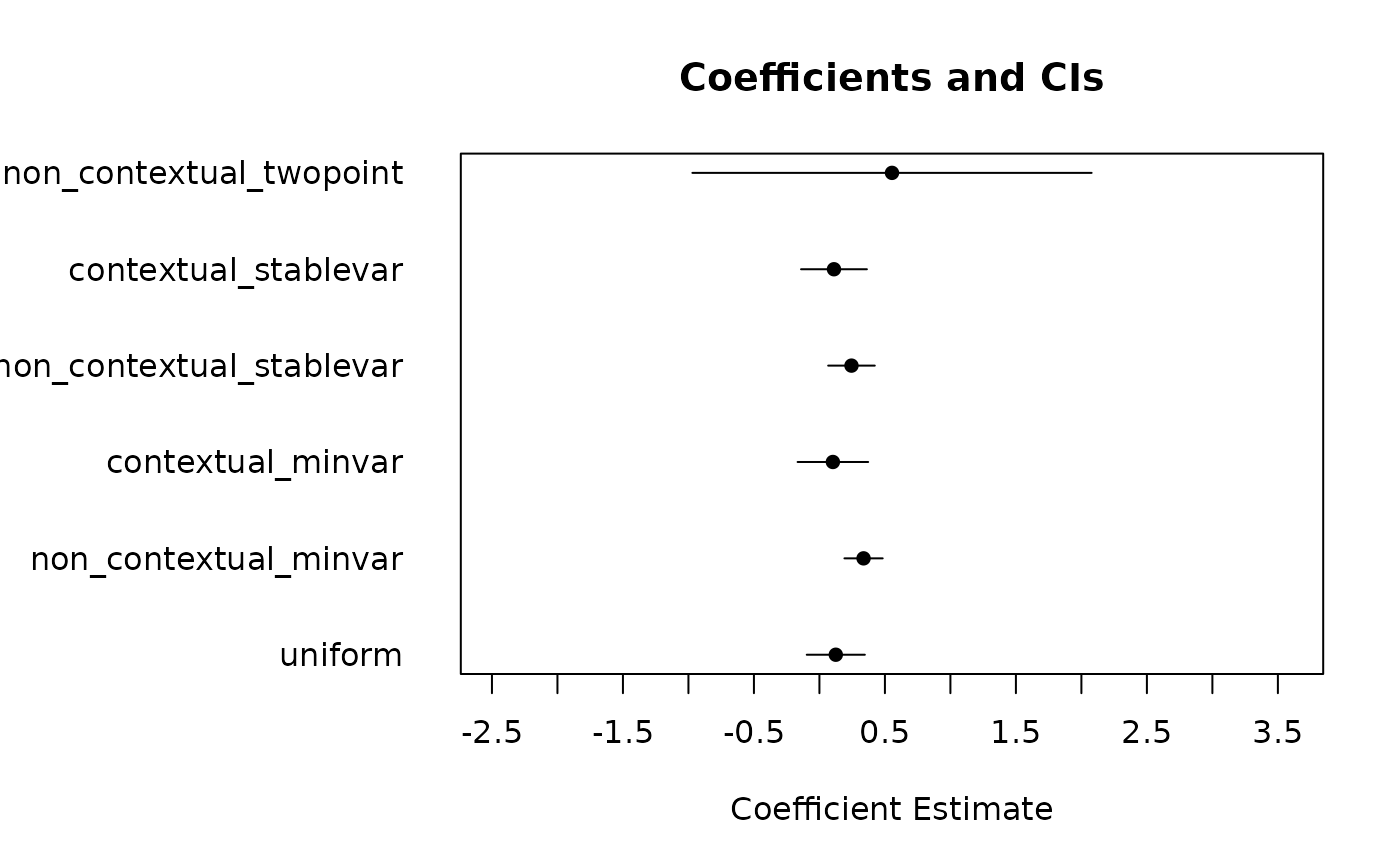par(op)